شرح درس التبرير الاستقرائي والتخمين أول ثانوي مسارات الرياضيات

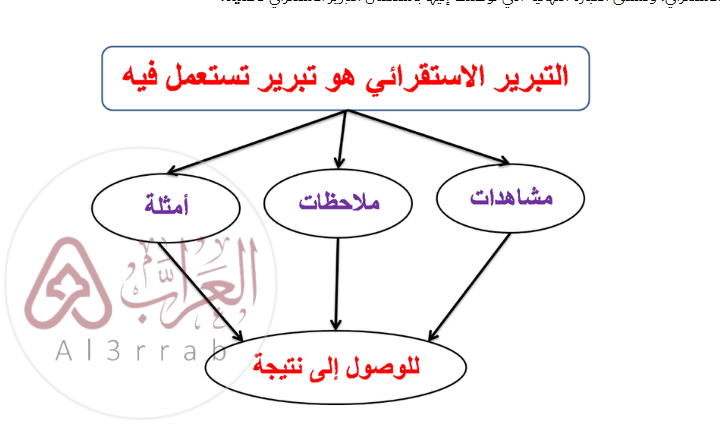
شرح درس التبرير الاستقرائي والتخمين أول ثانوي مسارات الرياضيات ، في أبحاث التسويق، يتم تحليل إجابات مجموعة من الأشخاص على أسئلة محددة حول منتج ما، ومن ثم يتم البحث عن نمط معين في الإجابات حتى يتم التوصل إلى نتيجة. وتسمى هذه العملية الاستدلال الاستقرائي.
ما هي الأشياء التي يبحث عنها باحث التسويق؟
مبيعات المنتجات ومقارنتها بالمنتجات المنافسة.
لماذا يقوم الباحث بطرح الأسئلة على مجموعة من الأشخاص فقط؟
غالبًا ما يكون من الصعب طرح الأسئلة على جميع المستهلكين، لذا قم بتوجيه الأسئلة إلى مجموعة مماثلة.
شرح درس التبرير الاستقرائي والتخمين أول ثانوي مسارات الرياضيات
إنه مبرر يتم فيه استخدام أمثلة محددة للوصول إلى نتيجة. عندما تفترض أن النمط سيستمر، فإنك تستخدم الاستدلال الاستقرائي، والبيان النهائي الذي تصل إليه باستخدام الاستدلال الاستقرائي يسمى التخمين.
الاستنتاج الذي يتم التوصل إليه من التبرير الاستقرائي يسمى التخمين.
مثال:
اكتب تخمينًا يصف النمط في كل من المتتابعات التالية، ثم استخدمه لإيجاد الحد التالي في كل منها.
1- مواعيد وصول الحافلات إلى محطة الصعود هي:
8:30 صباحًا، 9:10 صباحًا، 9:50 صباحًا، 10:30 صباحًا، …….
الحل:
الخطوة الأولى: العثور على نمط.
8:30 صباحًا، 9:10 صباحًا، 9:50 صباحًا، 10:30 صباحًا……….
40 دقيقة 40 دقيقة 40 دقيقة
الخطوة 2: قم بالتخمين.
تصل الحافلة بعد 40 دقيقة من وصول الحافلة السابقة. موعد وصول الحافلة التالية هو الساعة 10:30 صباحًا + 40 دقيقة، أي الساعة 11:10 صباحًا
وبالتالي فإن الجواب هو: الساعة 11:10 صباحاً
التمرين 1:
اكتب تخمينًا يصف النمط في كل من المتتابعات التالية، ثم استخدمه للعثور على الحد التالي في كل منها:
الأشهر المتتابعة: صفر، رجب، ذو الحجة، جمادى الأولى،….
الجواب: شوال
توضيح: الشهر التالي في التسلسل يأتي بعد خمسة أشهر من الشهر السابق.
10، 4، -2، -8، …………
الجواب: 14-
توضيح: الرقم التالي في التسلسل أقل بـ 6 من الرقم السابق.

الاجابة هي:
الإيضاح: يقسم كل مثلث مظلل في الشكل السابق إلى أربع مثلثات متطابقة الأضلاع يتوسطها مثلث أبيض.

مثال:
قم بالتخمين الذي يصف النمط في كل من المتتاليات التالية، ثم استخدمه للعثور على الحد التالي في كل منها.
2، 4، 12، 48، 240، …………. (أ
الجواب: 1440
التخمين: اضرب الحد النوني في n+1 لتحصل على الرقم التالي 1440.
تمرين 2:
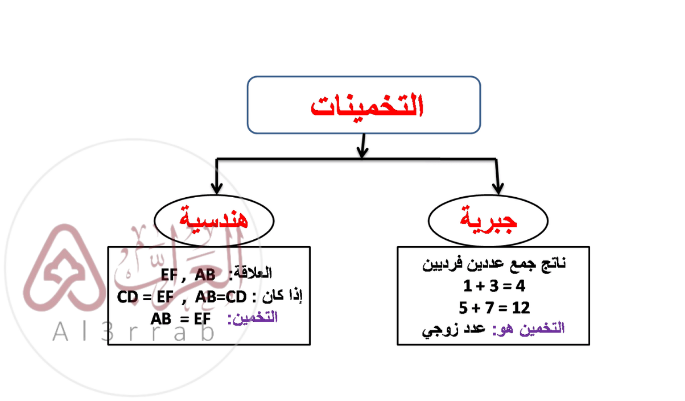
قم بتخمين كل قيمة أو علاقة هندسية لكل مما يلي، مع إعطاء أمثلة عددية أو رسم أشكال تساعد في الوصول إلى هذا التخمين.
1- نتيجة جمع رقمين زوجيين.
الحل:
6 = 2 + 4
18 = 10 + 8
10 = 6 + 4
وينتج عن ذلك أن مجموع رقمين زوجيين هو عدد زوجي
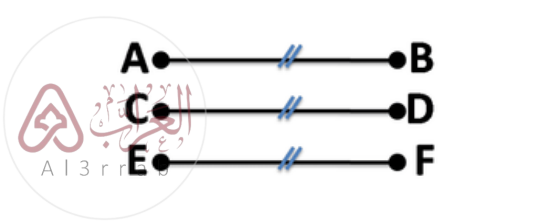
العلاقة بين AB و EF، إذا كانت: CD = AB و EF = CD
ينتج أن: AB = EF
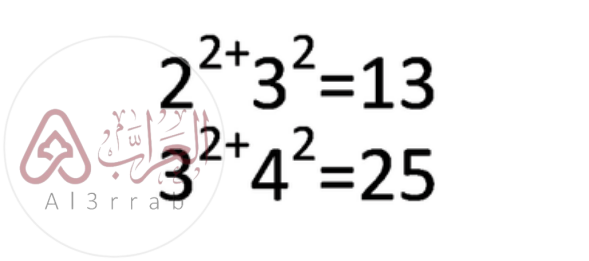
المجموع المربع لعددين صحيحين متتاليين
الحل: مجموع مربعي عددين صحيحين متتاليين هو عدد فردي
إذن مجموع مربعي عددين صحيحين متتاليين هو عدد فردي.
تعتمد التخمينات في مواقف الحياة الواقعية على البيانات المجمعة حول موضوع التخمين.
مثال:
والجدول المجاور يوضح أسعار المنتج خلال الأعوام من 1402هـ إلى 1427هـ.
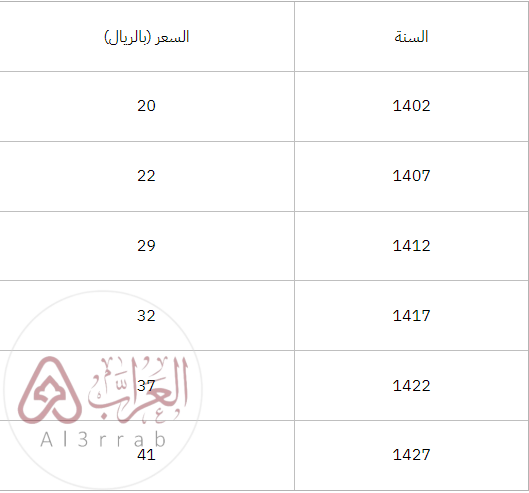
أنشئ التمثيل البياني الأنسب لعرض هذه البيانات
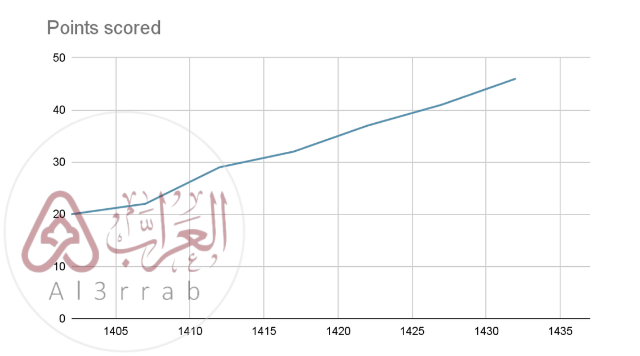
تخمين سعر المنتج في عام 1432 هـ
ومن الرسم نجد أن عام 1432هـ يقابل قيمة 46
فالجواب: 46 ريالاً تقريباً
فهل من المعقول أن نقول إن هذا النمط سيستمر مع مرور الوقت؟ إذا لم يكن الأمر كذلك، كيف سيتغير؟
نعم، هذا الاتجاه المتزايد معقول، لأن سعر المنتج من المرجح أن يستمر في الارتفاع على مر السنين.
يتطلب إثبات صحة تخمين معين في جميع الحالات تقديم دليل على هذا التخمين. أما لإثبات عدم صحة التخمين فيكفي تقديم مثال واحد مضاد للتخمين، وقد يكون رقماً أو رسماً أو عبارة، وهذا المثال المعاكس يسمى مثالاً مضاداً.

التمرين 3:
أعط مثالا مضادا لتوضيح أن كل من التخمينات التالية خاطئة.
1- إذا كان n عدداً حقيقياً، فإن n- يكون سالباً.
نعطي مثالا: n عدد حقيقي = 2-
ن=-2 ⇒ -ن = – (-2) = 2
هذا أعطانا رقمًا موجبًا (مثال مضاد).
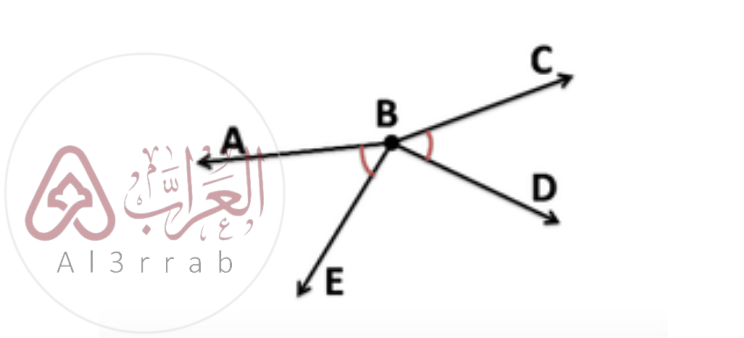
2- ∠ABE > ≅ DBC إذا كان لدينا
∠ABE و∠DBC متقابلان رأسيًا.
عندما تقع النقاط أ، ب، د على نفس الخط
النقاط E وB وC لا تقع على خط واحد
التخمين خاطئ
في الشكل التالي، ABE ≅∠DBC⦣، لكن ABE⦣ وDBC⦣ ليسا متقابلين رأسيًا.