قيم x , y التي تجعل الشكل الرباعي المجاور متوازي أضلاع هي

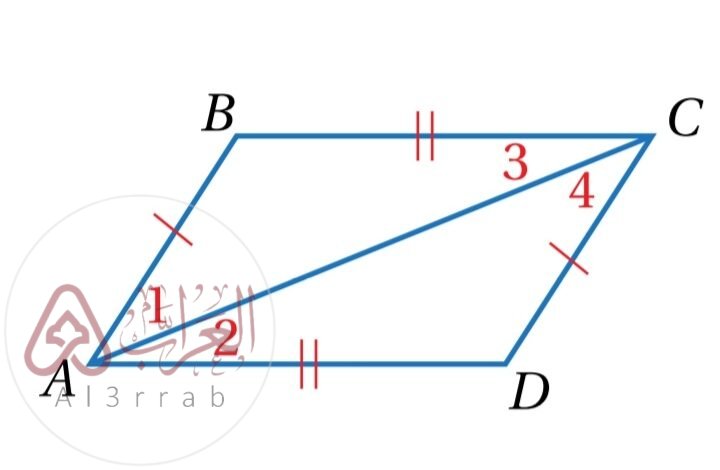
قيم x , y التي تجعل الشكل الرباعي المجاور متوازي أضلاع هي

في هذا المقال سنشرح الفكرة بأسلوب مبسط، مع أمثلة توضيحية تساعدك على الحل بسهولة.

ما هو متوازي الأضلاع؟

متوازي الأضلاع هو شكل رباعي يتميز بـ:

• كل ضلعين متقابلين فيه متوازيان ومتساويان في الطول.
• كل زاويتين متقابلتين فيه متساويتان في القياس.
• القطران فيه ينصف كل منهما الآخر.

متى يكون الشكل الرباعي متوازي أضلاع؟

لكي يكون الشكل الرباعي متوازي أضلاع، يكفي تحقق أحد الشروط التالية:

• كل ضلعين متقابلين متوازيان.
• كل ضلعين متقابلين متساويان في الطول.
• كل زاويتين متقابلتين متساويتان.
• القطران ينصف كل منهما الآخر.

كيف نوجد قيم𝑥x و𝑦y؟

في المسائل غالبًا تُعطى أطوال أو زوايا بدلالة 𝑥x و𝑦y، مثلًا:

ضلع =3𝑥+23x+2 الضلع المقابل =2𝑥+62x+6

حتى يكون الشكل متوازي أضلاع:
نساوي الضلعين المتقابلين:

3𝑥+2=2𝑥+63x+2=2x+6𝑥=4x=4

وبنفس الطريقة إذا كانت الزوايا بدلالة𝑦y، نساوي الزوايا المتقابلة أو نستخدم أن مجموع زاويتين متجاورتين = 180°.

مثال محلول

إذا كان في الشكل الرباعي:

𝐴𝐵=2𝑥+4AB=2x+4𝐶𝐷=5𝑥
−
8CD=5x−8

لأنه متوازي أضلاع:

2𝑥+4=5𝑥
−
82x+4=5x−83𝑥=12⇒𝑥=4
3x=12⇒x=4
خلاصة المقال

✔ لإيجاد قيم
𝑥x و𝑦y التي تجعل الشكل الرباعي متوازي أضلاع:

ساوِ بين الأضلاع المتقابلة.

ساوِ بين الزوايا المتقابلة.

استخدم قاعدة أن الزوايا المتجاورة مجموعها 180°.